图的两种存储结构

邻接矩阵

图的邻接矩阵(Adjacency Matrix) 存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。

• 即有一个数组存储顶点

• 一个维数组存储各个顶点之间的关系，即是存储边的信息，比如权值

• 有向图和无向图的的矩阵存储不一样

比如下图，假如有一个是有n个顶点的图，则邻接矩阵是一个n*n的方阵，以下定义

)

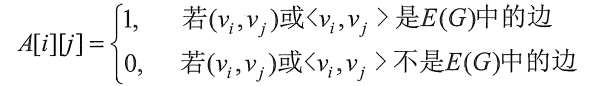无向图和他的邻接矩阵

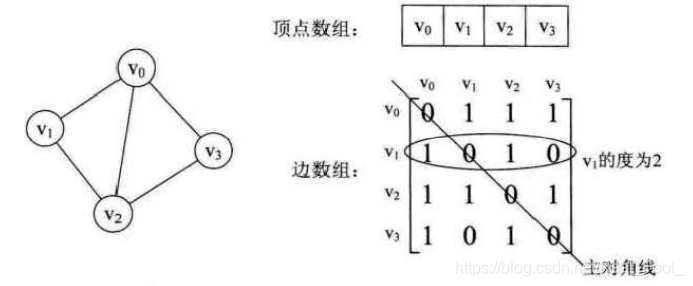
• 比如v1的顶点入度为1+1=2
• 求顶点v i 的所有邻接点就是将矩阵中第i行元素扫描一遍， A [ i ] [ j ] = 1就是邻接点
• 看vi是否和vj相连接，直接看是否A[i] [j]=1或者A[j] [i]=1都可以

有向图和它的邻接矩阵

有向图的矩阵并不是对称矩阵，看下图

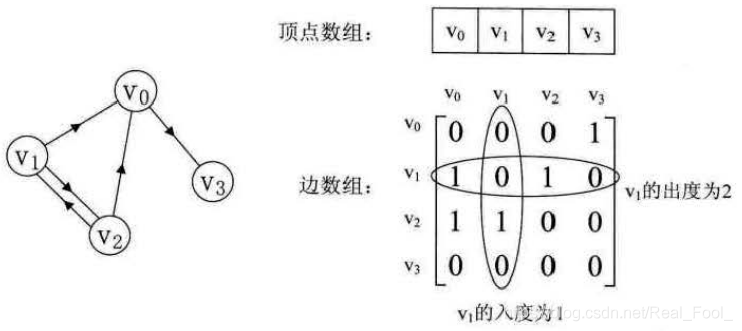
• 因为是有向图，所以入度和出度并不相同，比如v1的出度看数组的第一行不为一的数目，而入度则是看第一列不为一的数目，所以入度为1而出度为2
• 判断顶点v i到v j 是否存在弧，只需要查找矩阵中A [ i ] [ j ]是否为1即可

对于带权值的有向图

vi和vj之间有链接的话，则相应的A[i] [j]=权值，即看下图

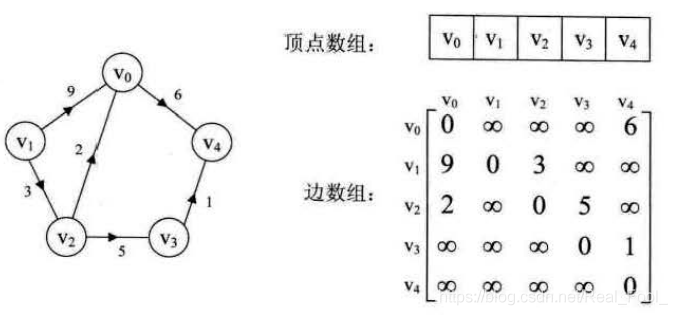
• 相连的话，相对应的A[i] [j]则用权值表示

• 如果不相连则用
  $$
  \infty
  $$

表示以下是一个图的简单定义

#define MaxVertexNum 100	//顶点数目的最大值
typedef char VertexType;	//顶点的数据类型
typedef int EdgeType;	//带权图中边上权值的数据类型
typedef struct{
	VertexType Vex[MaxVertexNum];	//顶点表
	EdgeType Edge[MaxVertexNum][MaxVertexNum];	//邻接矩阵，边表
	int vexnum, arcnum;	//图的当前顶点数和边数
}MGraph;

邻接表

当一个图的边数太少用邻接矩阵的方式存储，太浪费空间，如下

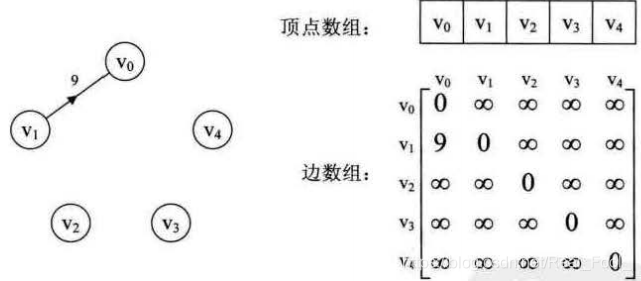
• 邻接表对于每一个顶点vi都建立了一个单链表，链表每个节点都存储着与vi相连的顶点信息，比如v1的单链表中有一个节点存储着v2的信息，则代表v1—–>v2(当为无向图时表示v1————v2)

• 所以邻接表共有两种表结构

  1. 一个是顶点表存储顶点信息，同时存储着指向相应链表的指针，
  2. 一个是边表存储边的信息，存储被指向的节点和权值

如下图

对于无向图的实例如下

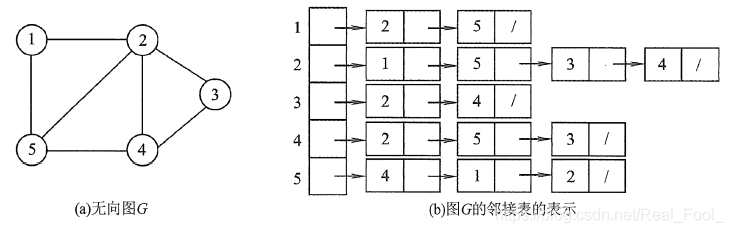
对于有向图的实例如下

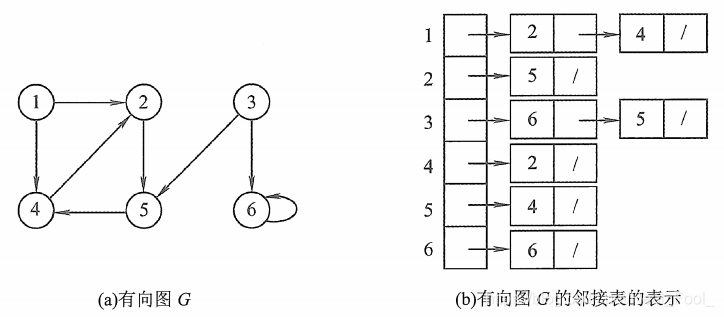
而代码实例如下

#define MAXVEX 100	//图中顶点数目的最大值
type char VertexType;	//顶点类型应由用户定义
typedef int EdgeType;	//边上的权值类型应由用户定义
/*边表结点*/
typedef struct EdgeNode{
	int adjvex;	//该弧所指向的顶点的下标或者位置
	EdgeType weight;	//权值，对于非网图可以不需要
	struct EdgeNode *next;	//指向下一个邻接点
}EdgeNode;

/*顶点表结点*/
typedef struct VertexNode{
	Vertex data;	//顶点域，存储顶点信息
	EdgeNode *firstedge	//边表头指针
}VertexNode, AdjList[MAXVEX];

/*邻接表*/
typedef struct{
	AdjList adjList;
	int numVertexes, numEdges;	//图中当前顶点数和边数
}

这里对于图的存储结构只做简单的介绍，如果要了解更多性质自行查找