拓扑排序的简单介绍

拓扑排序

关于拓扑排序

拓扑排序通俗点来说就是对于一个有向无环图(DAG)来说，不断输出其入度为0的节点直到不存在，每个节点输出一次且仅有一次

拓扑排序用官方的话来说就是：对一个有向无环图(DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边<u,v>∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

执行步骤

拓扑排序主要步骤，也就主要循环两部分到不存在入度为零的顶点为止

• 选择一个入度为零的顶点输出
• 在AOV网中删除这个顶点及其出边

输出结束后，除非还有回路，否则其输出的顶点序列就是拓扑排序

AOV网其实就是有向无回路图，就是DAG

图解

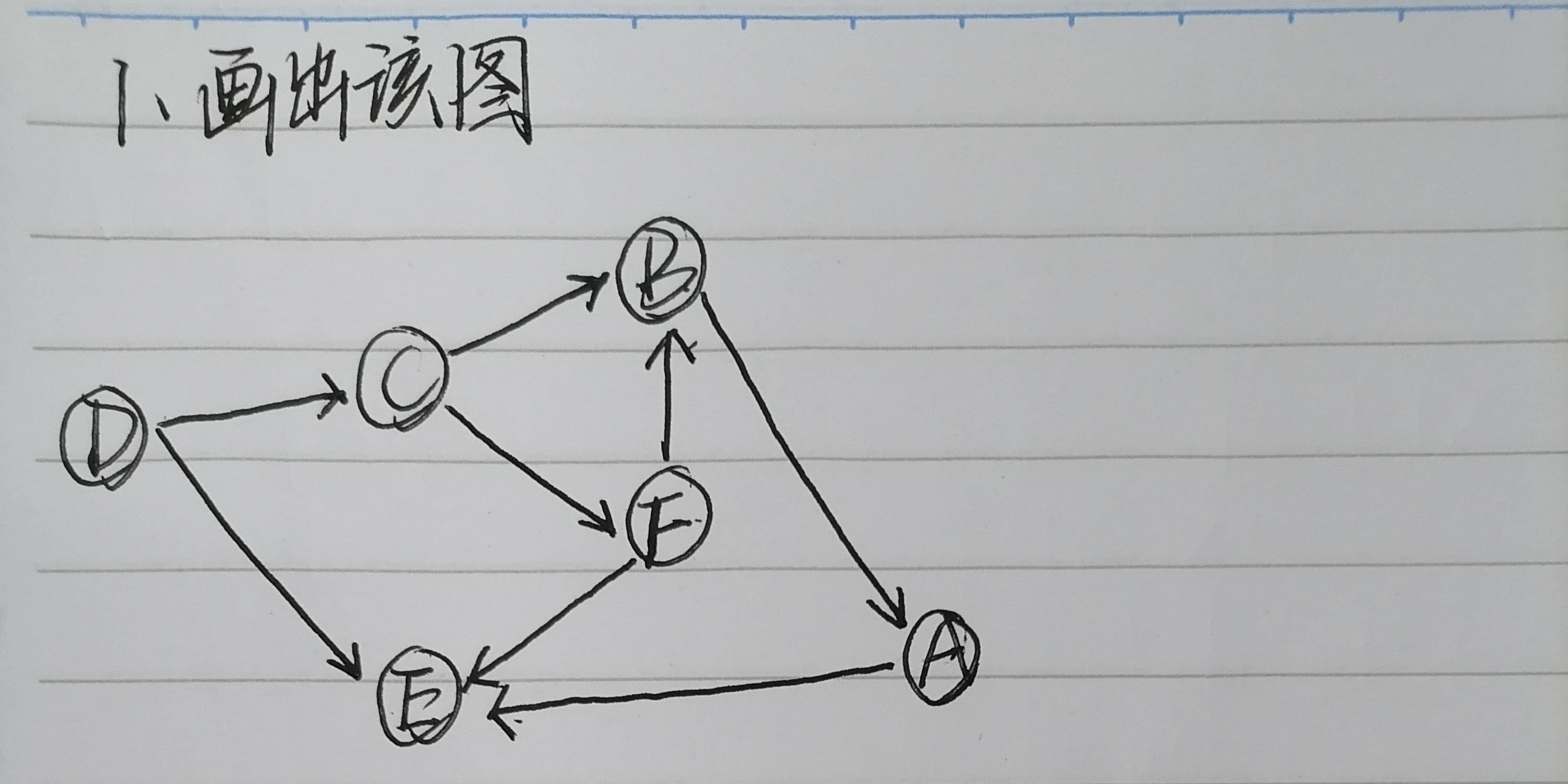
对于以下图来说

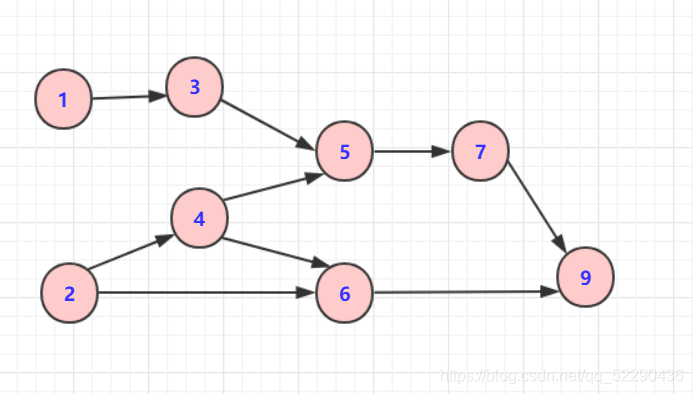
删除1和2顶点和其对于边后并且输出，并且以此类推

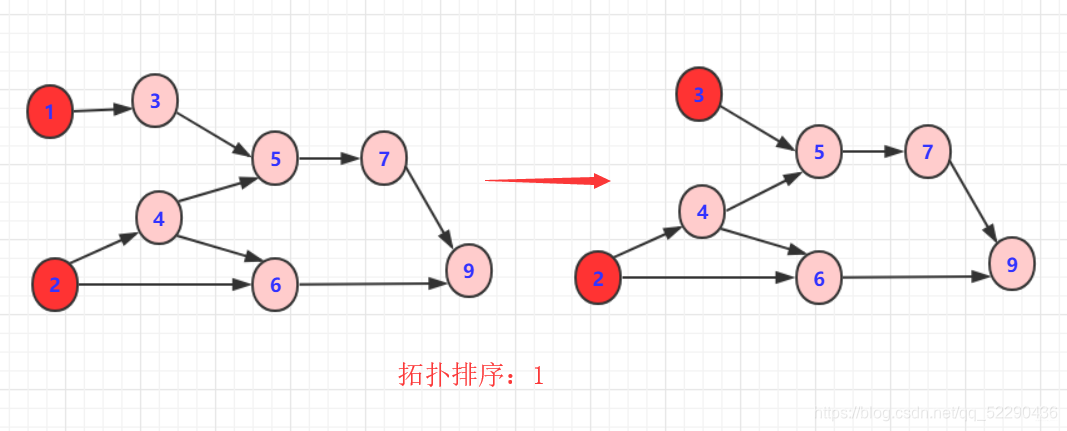
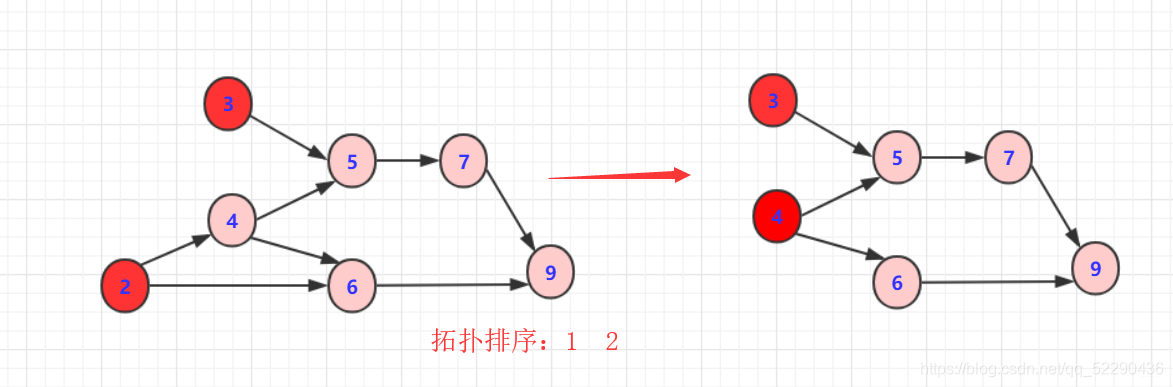
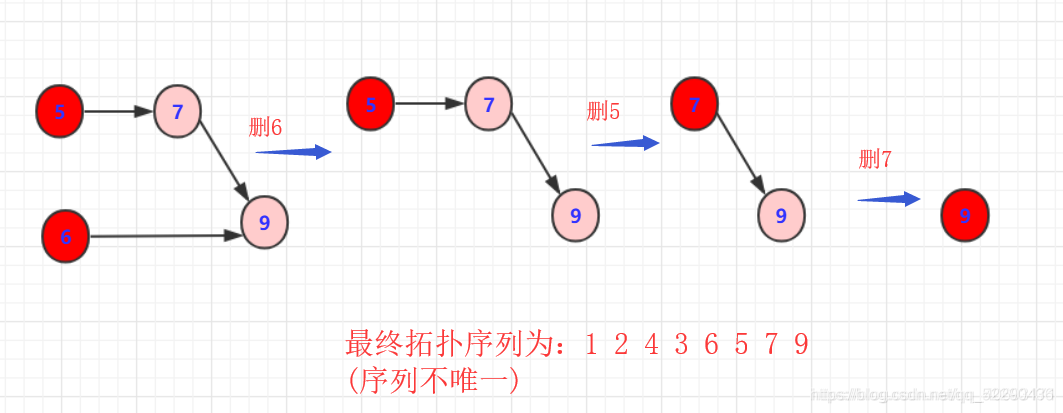
其实对于输出的序列不唯一就看你自己怎么样设计栈的结构

代码实现

这里使用邻接表实现，再利用栈实现入度为零的输出

使用作业的题目，ABCDEF对应下标从0开始慢慢增大

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAXVEX 10
typedef char VerType;	//顶点值类型

struct EdgeNode{
	int adjvex;	//邻接点域，存储该顶点对应的下标
	int weight;	//用于存储权值，对于非网图可以不需要
	struct EdgeNode* next;	//下一个结点
};

struct VertexNode{
	int in;	//入度
	VerType data;	//值
	struct EdgeNode* firstedge;	//邻接表头指针
};

struct Graph{
	struct VertexNode vers[MAXVEX];
	int numVertexes, numEdges;	//顶点数和边数
};

/* 拓扑排序，若G没有回路，则输出拓扑排序序列并返回OK，若有回路返回ERROR */
int  TopologicalSort(struct Graph* G){
	struct EdgeNode* e;
	int i, k, gettop;
	int top = 0;	//栈指针下标
	int count = 0;	//统计输出顶点个数
	int* stack;	//存储入度为0的顶点
	stack = (int*)malloc(G->numVertexes * sizeof(int));

	for(i = 0;i<G->numVertexes;i++)	//遍历所有结点
		if(G->vers[i].in == 0)
			stack[++top] = i;	//将入度为0的顶点入栈

	while(top != 0){
		gettop = stack[top--];	//出栈
		printf("%c ",G->vers[gettop].data);
		count++;	//统计输出顶点数
		for(e=G->vers[gettop].firstedge; e; e = e->next){
			//弧表遍历
			k = e->adjvex;
			if(!(--G->vers[k].in))	//将k号顶点邻接点的入度减1
				stack[++top] = k;	//若为0则入栈，以便下次循环输出
		}
	}
	if(count < G->numVertexes)	//如果count小于顶点数，说明存在环
		return 0;
	else
		return 1;
}

/* 图初始化 */
void CreateGraph(struct Graph* G){
	int i, m, n;

	printf("输入顶点数和边数：\n");
	scanf("%d %d",&G->numVertexes, &G->numEdges);
	printf("输入顶点值：\n");
    getchar();	//吃掉回车
	for(i=0;i<G->numVertexes;i++){
		//getchar();	//吃掉回车
		G->vers[i].data=getchar();
		getchar();
		//scanf("%c",&G->vers[i].data);
	}
	//初始化图头结点指针和入度值
	for(i=0;i<G->numVertexes;i++){
		G->vers[i].firstedge = NULL;
		G->vers[i].in = 0;	//入度为0
	}
	printf("输入边：\n");
	for(i=0;i<G->numEdges;i++){
		scanf("%d %d",&m, &n);
		struct EdgeNode *newNode = (struct EdgeNode*)malloc(sizeof(struct EdgeNode));
		newNode->next = G->vers[m].firstedge == NULL ? NULL : G->vers[m].firstedge;
		newNode->adjvex = n;
		G->vers[m].firstedge = newNode;
		G->vers[n].in++;	//入度+1
	}
}

int main(){

	struct Graph *G=(struct Graph*)malloc(sizeof(struct Graph)) ;
	CreateGraph(G);
	if(TopologicalSort(G)){
		printf("拓扑排序完成！\n");
	}else{
		printf("图存在环");
	}
	return 0;
}